We need to calculate the following sum:
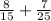
The first step is to calculate the least common multiplier between the two denominators. This is done below:
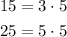
We broke down the two denominators into their factors, now we need to multiply the factors that are unique. This is done below:
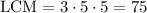
Now we have to replace the denominators by 75 and calculate new numerators. The new numerators must be calculated as follows:
1 - Divide the LCM by the old denominator
2 - Multiply the result of 1 by the old numerator.
This is done below:
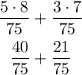
Since both fractions have their denominators with the same value, we can just directly add them.
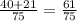
The fraction is already in its most reductable form, therefore the answer is 61/75.