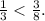To rewrite the fractions as fractions with the same denominator we have to determine the minimum number greater than 8 and 3 that can be exactly divided by 8 and 3 (LCM). Notice that the LCM of 8 and 3 is
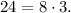
Because:
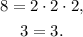
Therefore, we rewrite the given fractions as:
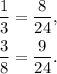
From the above fractions, we get that:

Answer:
a)
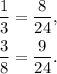
b)