Question

At any time t (in hours), there are 216(t +18) of Type A bacteria in a sample and 362t + 8 of Type B bacteria in a sample. After how many hours will the number of type A bacteria be less than the type B bacteria?

Answer 1

1. The given situation can be described in the following inequality:

`216^((t+18))<36^((2t+8))`

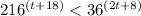
2. To solve the prevous inequality, proceedas follow:

write 216 as 6^3 and 36 as 6^2, then, apply log_6 both sides:

`\begin{gathered} 6^(3(t+18))<6^(2(2t+8)) \\ \log _66^(3(t+18))<\log _66^(2(2t+8)) \\ 3(t+18)<2(2t+8) \end{gathered}`

then, solve for t, as follow:

`\begin{gathered} 3t+54<4t+16 \\ 3t-4t<16-54 \\ -t<-38 \\ t>38 \end{gathered}`

Hence, from t = 38 hours the number of type A bacteria will be less than the type B bacteria

3. In a number line, you obtain: