We have a rectangular box where we know the area of the faces and we have to find the width w, length l and height h.
The area of the top of the box is equal to the length times the width (l*w) and we also know that it is 42 cm², so we can write:
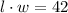
With the same logic, we can write the equations for the other two areas:
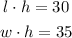
NOTE: the area we choose for l or w is indistinct,so we can relate it as we like.
Then, we can solve this system of equations substituting variables as:
![\begin{gathered} l\cdot h=30\longrightarrow l=(30)/(h) \\ w\cdot h=35\longrightarrow w=(35)/(h) \\ l\cdot w=((30)/(h))((35)/(h))=(1050)/(h^2)=42 \\ h^2=(1050)/(42) \\ h^2=25 \\ h=\sqrt[]{25} \\ h=5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/3gvqrmkop3mtymvgl97wb6zjn3smqunfqm.png)
With the value of h, we can calculate l and w:
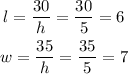
Answer:
The dimensions of the box are: length = 6 cm, width = 7 cm and height = 5 cm.