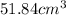The volume of a prism can be calculated by multiplying the area of the base of the prism times its height:
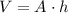
On the other hand, the area of the base of a triangle can be found by multiplying 1/2 times its base times its height (don't confuse the height of the triangle with the height of the prism):
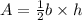
Substitute the values for the base of the triangle and its height to find the area of the base. Then, substitute the result for the area and the value of the height of the prism to find the volume of the triangular prism.
If the base of the triangle has a length of 5.4cm, and its height is 3.2cm, then:
![\begin{gathered} A=(1)/(2)*5.4\operatorname{cm}*3.2\operatorname{cm} \\ =8.64cm^2 \end{gathered}]()
If the height of the prism is 6cm, then its volume is:
![\begin{gathered} V=8.64cm^2*6\operatorname{cm} \\ =51.84cm^3 \end{gathered}]()
Therefore, the volume of the triangular prism, is: