We know that the mean score obtained by the freshman students last year was 1140.
It means that the sum of all the freshman students' scores from last year, divided by the number of freshmen students resulted in the number 1140.
It doesn't mean necessarily that one or more students had a score of exactly 1140.
Step 1
Find an example showing that some of the statements must not be true.
A way of obtaining this score is if half the N students had a score of 0, and the other half had a score of 2280:
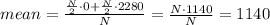
From this example, none of the students had a score of exactly 1140, and half of them had a score less than 1140. So, we can conclude that the first three statements must not be true.
Step 2
Analyze the other statements.
The fourth statement must not be true because we can't conclude anything for sure for next year's scores based on the last year's scores.
Let's analyze the fifth statement. Suppose it must not be true, i.e., all the freshman students had scores equal to or less than 900. Then, since the mean score can't be greater than the maximum score, the mean score would be no more than 900. Wich is false because it was 1140 > 900.
Therefore, the fifth statement must be true.
Answer
The only claim that must be true is:
Last year, at least one of their freshman students had a score of more than 900 on the exam.