Question

The half-life for the first order radioactive decay of lodine - 131 is 8.0 days. After 3 half lives, what percentage of a sample of locine-131)remains?O 50.%O 25%,O 12.5%O 1%

Answer 1

12.5 %.

Step-by-step explanation:

Let's see the half-life formula:

`N(t)=N_0\cdot((1)/(2))^{t\text{/h}}.`

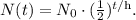
Where N₀ is the initial amount, t is time, and h is the half-life.

We want to know what would be the percentage of a sample of iodine-131 that remains. This is the same that N(t)/N₀, so we have to replace the given data in the formula and multiply it by 100 because it is a percentage.

The half-life of iodine-131 is 8.0 days, and 3 half-lives are equal to 24 days (8.0 x 3 = 24):

`\begin{gathered} (N(t))/(N_0)=((1)/(2))^{t\text{/h}}, \\ ((1)/(2))^{24\text{/8}}=((1)/(2))^3=(1)/(8)=0.125. \\ We\text{ want the result in percentage, so multiplying by 100}\%,\text{ we obtain:} \\ 0.125\cdot100\%=12.5\%. \end{gathered}`

The answer would be 12.5 %.