Question

8.The outfield fencing for a Minor League field forms a circular sector with home plate as thecenter. (See the figure at the top of page 681.) The fence is placed at a uniform distance of2130 ft from home plate. The boundaries of the fence, which extends partway into foulterritory, create an angle of 110 degrees with home plate. At $21 per foot, how much willthe fence cost? (Round to the nearest $10.)

Answer 1

The Solution.

Representing the problem in a diagram, we get

To find the length of the boundaries of the fence, we shall use the formula below:

`\begin{gathered} \text{Length}=(\theta)/(360)*2\pi r \\ \text{Where }\theta=110^o \\ \pi=3.14 \\ r=2130\text{ ft} \end{gathered}`

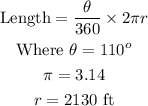
Substituting these values in the formula, we get

`\begin{gathered} \text{Length}=(110)/(360)*2*3.14*2130 \\ \\ \text{ =}(11*3.14*2130)/(18)=4087.23\text{ fe}et \end{gathered}`

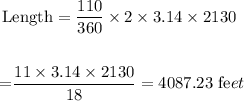
We were told that each foot cost $21.

So, the cost of the fence is

`(4087.23)/(21)=\text{ \$194.63}\approx\text{ \$190}`

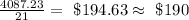
Therefore, the correct answer is $190