Hello there. To solve this question, we have to remember some properties about logarithms.
Given the logarithmic equation:
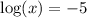
We want to determine the value of x.
For this, remember the following rule:
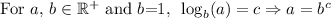
Such that, in this case, the logarithm has base 10, therefore
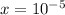
This power of 10 can be easily found :
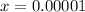
It has 5 digits after the decimal place, being the fifth digit a 1.
This is the answer contained in the option B.