Given:
Sample size = 100
p = 30% = 0.30
p' = 25% = 0.25
Let's find the probability that a sample proportion will over- or under-estimate the parameter by more than 5%.
Here, the error is:
Errror = |p' - p| = |0.25 - 0.30| = |-0.05| = 0.05
This error is not surprising.
Now, apply the formula:
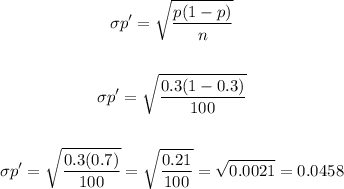
Now, to find the probability that a sample proportion will be over or underestimate more than 5% will be:
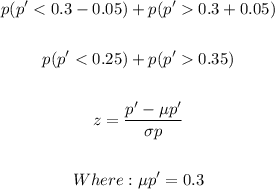
Hence, we have:
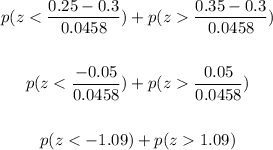
Using the standard normal distribution table, we have:
NORMSDIST(-1.09) =0.1379
NORMSDIST(1.09) = 0.8621
Hence, we have:
p(z<-1.09) = 0.1379
p(z>1.09) = 1 - 0.8621 = 0.1379
p(z<-1.09) + p(z>1.09) = 0.1379 + 0.1379 = 0.2758
Therefore, the probability is 0.2758.
ANSWER:
0.2758