Question

I have some problems applying the formulas to solve physics problems. I understand all the concepts needed, but just freeze when I see questions, especially when it comes to trying to combine linear and rotational conceptsA uniform, 255 N rod that is 1.90 m long carries a 225 N weight at its right end and an unknown weight W toward the left end (Figure 1). When W is placed 60.0 cm from the left end of the rod, the system just balances horizontally when the fulcrum is located 75.0 cm from the right end.1) Find W.2) If W is now moved 30.0 cm to the right, how far must the fulcrum be moved to restore balance?

Answer 1

`\begin{gathered} 1)\text{ }214.90\text{ }N \\ \\ 2)\text{ }0.09\text{ }m \end{gathered}`

Step-by-step explanation

First, let us make a sketch of the diagram showing the distances on the rod:

1) Since the fulcrum is balanced, the center of gravity of the system will be at the fulcrum.

The center of gravity (in the horizontal is given by:

`x=(W_1x_1+W_2x_2+W_3x_3)/(W_1+W_2+W_3)`

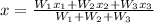
where W1 = the weight on the right end = 225 N

W2 = the weight of the rod = 255 N

W3 = the weight place on the left = W

x1 = the position of W1 (taking the left as the origin) = 1.90 m

x2 = the position of the center of mass of the rod = x1/2 = 0.95 m

x3 = the position of W from the left end = 0.60 m

x = position of center of gravity of the rod from the left end i.e. at the fulcrum = 1.90 - 0.75 = 1.15 m

Now, substitute the values given in the question and solve for W:

`\begin{gathered} 1.15=((225*1.90)+(255*0.95)+(W*0.60))/(225+255+W) \\ \\ 1.15=(427.5+242.25+0.60W)/(480+W) \\ \\ 1.15(480+W)=669.75+0.60W \\ \\ 552+1.15W=669.75+0.60W \\ \\ 1.15W-0.60W=669.75-552 \\ \\ 0.55W=117.75 \\ \\ W=(117.75)/(0.55) \\ \\ W=214.09\text{ }N \end{gathered}`

That is the value of W.

2) Now, W is moved 30.0 cm (0.30 m) to the right.

This implies that:

`x_3=0.60+0.30=0.90\text{ }m`

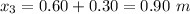
Since the other values (including W) do not change, we can now solve for x, which is the new center of gravity:

`\begin{gathered} x=((225*1.90)+(255*0.95)+(214.09*0.90))/(225+255+214.09) \\ \\ x=(427.5+242.25+192.681)/(694.09)=(862.431)/(694.09) \\ \\ x=1.24\text{ }m \end{gathered}`

Therefore, the fulcrum must be moved:

`\begin{gathered} 1.24\text{ }m-1.15\text{ }m \\ \\ 0.09\text{ }m \end{gathered}`

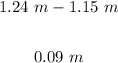
The fulcrum should be moved 0.09 m to the right (since the W is moved to the right).