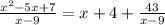The expression is:
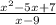
Part B
To get -9 to -5, we need to add 4. This is important because the factored form will be something like this:
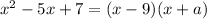
And when we distribute it, the middle term will be the sum of -9 and a, so we if we want it to be -5 (as the given expression) a has to be 4.
Part C
Now, looking to the constant part, it will be the multiplication of -9 and a, since we know that a is 4, the constant term is:
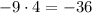
So, we need a constant term of -36 in the numerator.
Part D
Since we already got 7 in the numerator, we have to add -43 to get it to -36.
Part E
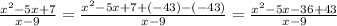
Part F
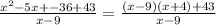
Part G

Part H
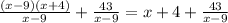
So: