Remember that
If f is continuous over [a,b] and differentiable over (a,b), then there exists c∈(a,b) such that
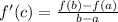
In this problem, we have the function
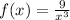
over the interval [1,3]
so
f(a)=f(1)=9/(1)^3=9
f(b)=f(3)=9/(3)^3=1/3
substitute
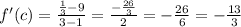
Find out the first derivative f'(x)
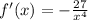
Equate the first derivative to -13/3
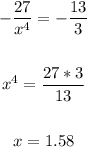
therefore
The value of c is 1.58 (rounded to two decimal places)