Question

Consider the following functions. Find four ordered pairs that satisfy the function

Answer 1

Since the function f(x) is

`f(x)=\sqrt[]{x-7}`

Since there is no square root for negative numbers, then

`x-7\ge0`

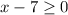
We will solve it by adding 7 to both sides

`\begin{gathered} x-7+7\ge0+7 \\ x\ge7 \end{gathered}`

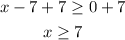
Then we can choose values of x from 7 and greater

Let x = 7

`\begin{gathered} f(7)=\sqrt[]{7-7} \\ f(7)=\sqrt[]{0} \\ f(7)=0 \end{gathered}`

The 1st ordered pair is (7, 0)

Let x = 11

`\begin{gathered} f(11)=\sqrt[]{11-7} \\ f(11)=\sqrt[]{4} \\ f(11)=2 \end{gathered}`

The 2nd ordered pair is (11, 2)

Let x = 8

`\begin{gathered} f(8)=\sqrt[]{8-7} \\ f(8)=\sqrt[]{1} \\ f(8)=1 \end{gathered}`

The 3rd ordered pair is (8, 1)

Let x = 16

`\begin{gathered} f(16)=\sqrt[]{16-7} \\ f(16)=\sqrt[]{9} \\ f(16)=3 \end{gathered}`

The 4th ordered pair is (16, 3)

The 4 ordered pairs are (7, 0), (8, 1), (11, 2), (16, 3)