The derivative of the function is given as:
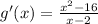
It is also given that g(3)=4.
Note that the Slope of a Tangent Line to a function at a point is the value of the derivative at that point.
Substitute x=3 into the derivative:
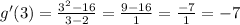
It follows that the slope of the tangent line at x=3 is -7.
Since it is given that g(3)=4, it implies that (3,4) is a point on the line.
Recall that the equation of a line with slope m, which passes through a point (x₁,y₁) is given by the point-slope formula as:
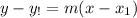
Substitute the point (x₁,y₁)=(3,4) and the slope m=-7 into the point-slope formula:

Hence, the equation of the tangent line to the graph of g at x=3 is y=-7x+25.
The required equation is y=-7x+25.