Question

Writing an equation of an… Given the foci and major axis length

Answer 1

We need to find the equation of the ellipse given the foci and major axis.

The equation is given by:

`((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1`

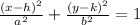
We have the foci points at (2,4) and (2,-6). The distance is 10 units, then the center is equal to half value c=5.

If the length of the major axis is 12.

Major axis length = 2a

Then

12 = 2a

a=12/2

a=6

To find b, we have the next equation:

`\begin{gathered} b^2=a^2-c^2 \\ Replacing \\ b^2=6^2-5^2 \\ b^2=36-25 \\ b^2=11 \\ Solve\text{ for b} \\ b=\sqrt[]{11} \end{gathered}`

Now, the center c is given by the point (2,-1). This point is in the middle of both foci points

Finally, we can replace on the ellipse equation:

`\begin{gathered} ((x-h)^(2))/(a^(2))+((y-k)^(2))/(b^(2))=1 \\ Replacing,\text{ the result is} \\ ((x-2)^2)/(6^2)+\frac{(y-(-1))^2}{(\sqrt[]{11})^2}=1 \end{gathered}`