The Slope-Intercept form of the equation of a line is:

Where "m" is the slope of the line and "b" is the y-intercept.
In this case you know that "y" represents the number of books in Himanshu's home library and "x" represents the number of weeks.
In the graph you can identify that:

And you can also identify this point on the line:

Where:

Substitute these values into the equation

and solve for "m" in order to find the slope:
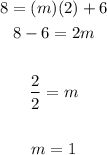
Then, the equation of this line is:

Based on the explained above, you can conclude that he had 6 books in his library and then he started adding 1 book each week.
To find the number of books he has after 4 weeks, you can make:

Substitute this value into the equation and evaluate. Then:
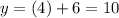
The answer is: Option A and Option F.