For this exercise you need to use the Work-rate formula. This is:
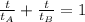
Where:
- "t" is the time for the objects A and B together.
- The individual time for object A is:
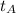
- The individual time for object B is:
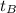
In this case, you can idenfity that:
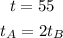
Substitute them into the formula:
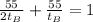
Now you must solve for:
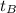
You get that this is:
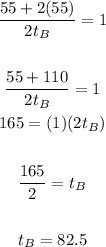
The answer is: It takes the smaller pipe 82.5 hours to fill the tank.