Step-by-step explanation
The question wants us to obtain the perimeter of the paperboard that remains after the semicircle has been removed
To do so, we will follow the steps below:
Step1: Find the Perimeter of the rectangle
The perimeter of a rectangle is simply the sum of all its sides
So in our case, we will have to sum sides A as given below
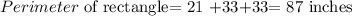
Step 2: Find the perimeter of the semi-circle
The perimeter of a semi-circle is given by:
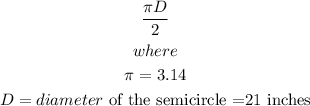
Simplifying

Step 3: Find the sum of the perimeters of the rectangle and semicircle
Therefore, the perimeter of the paperboard that remains after the semicircle is removed will be

Hence, the perimeter of the paperboard that remains after the semicircle is removed will be 119.97 in