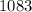Question

So, if you look at number 17 I need to know how to do the strategy so I can wright it down and study it for my test tomorrow! Will give 5 stars if you do an amazing explanation!

Answer 1

Question:

What is:

`51+5^2.31+18^2-9.7`

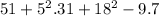
Solution:

Consider the following expression:

`51+5^2.31+18^2-9.7`

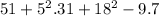
By precedence in arithmetic operations, we will first perform the powers:

`51\text{ + (25)(31)+(324)-(9)(7)}`

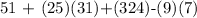
now, by precedence in arithmetic operations, we will perform the multiplications:

`51\text{ +775+324-}63`

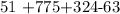
now, by precedence in arithmetic operations, we will perform the sums:

`(51\text{ +775+324)-}63`

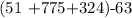
that is:

`1150-63`

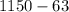
Finally, we perform the respective subtraction:

`1083`

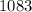
so that, we can conclude that the correct answer is:

`1083`