Question

The height of the triangle is 3 feet less than twice its base. The area of the triangle is 52 ft2. What is the height of the triangle?

Answer 1

Given:

Base of triangle = b

Height of triangle, h, is 3 feet less than twice its base. This is expressed as:

h = 2b - 3

Area of triangle = 52 ft²

To find the height of the triangle, use the Area of a triangle formula below:

`A=(1)/(2)bh`

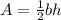
Thus, we have:

`\begin{gathered} 52=(1)/(2)* b*(2b-3) \\ \\ 52=(b(2b-3))/(2) \end{gathered}`

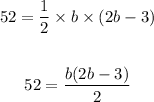
Let's solve for the base, b:

`\begin{gathered} 52=(2b^2-3b)/(2) \\ \\ Multiply\text{ both sides by 2:} \\ 52*2=(2b^2-3b)/(2)*2 \\ \\ 104=2b^2-3b \end{gathered}`

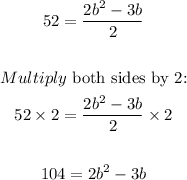
Subtract 104 from both sides to equate to zero:

`\begin{gathered} 2b^2-3b-104=104-104 \\ \\ 2b^2-3b-104=0 \end{gathered}`

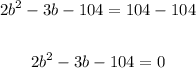
Factor the quadratic equation:

`(2b+13)(b-8)`

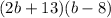
Thus, we have:

`\begin{gathered} (2b+13)\text{ = 0} \\ 2b\text{ + 13 = 0} \\ 2b=-13 \\ b=-(13)/(2) \\ \\ \\ (b-8)=0 \\ b=8 \end{gathered}`

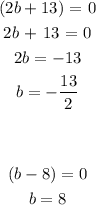
We have the possible values for b as:

b = - 13/2 and 8

Since the base can't be a negative value, let's take the positive value.

Therefore, the base of the triangle, b = 8 feet

To find the height, substitute b for 8 from the height equation, h=2b-3

Thus,

h = 2b - 3

h = 2(8) - 3

h = 16 - 3

h = 13 feet.

Therefore, the height of the triangle, h = 13 feet

ANSWER:

13 feet