Question

Team Arrow shoots an arrow from the top of a 1600-foot building on Earth-51. The arrow reaches a maximum height of 1840 feet after 4 seconds.Write an equation for the height of the arrow, h, in feet as a function of the number of seconds, t, since the arrow was shot.Round to 3 decimal places as needed. After how many seconds will the arrow reach the ground?Round to 3 decimal places as needed.

Answer 1

We will have the following:

***First:

`h=h_0+v_0\cdot t+(1)/(2)g\cdot t^2`

Now, we will determine the value for the speed:

`1840=1600+v_0\cdot(4)+(1)/(2)(-32.17)\cdot(4)^2\Rightarrow240=4v_0-(25736)/(25)`
`\Rightarrow(31736)/(25)=4v_0\Rightarrow v_0=(7934)/(25)\Rightarrow v_0=137.36`

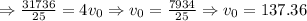
So, the equation for the height of the arrow (h) in feet as a function of the number of seconds t is:

`h=1600+317.36t+(1)/(2)gt^2`

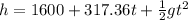
Here "g" is the gravitational pull of earth.

***Second:

We will determine how much time it would take for the arrow to hit the ground as follows:

`0=1600+317.36t+(1)/(2)(-32.17)t^2\Rightarrow-(3217)/(200)t^2+317.36t+1600=0`
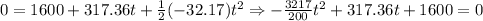
`\Rightarrow t=\frac{-(317.36)\pm\sqrt[]{(317.36)^2-4(-(3217)/(200))(1600)}}{2(-(3217)/(200))}\Rightarrow\begin{cases}t\approx-4.163 \\ t\approx23.893\end{cases}`

So, afeter 23.893 seconds the arrow would hit the ground.