Given data:
* The normal weight of the student is 500 N.
* The initial velocity of the student is 0 m/s at time 0 second.
Solution:
(a). For the time interval 0 to 5 seconds,
The scale reading is 500 N.
Thus, the force acting on the elevator is,
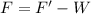
where F is the net force with which the elevator is moving in upward direction, F' is the scale reading (apparent weight), and W is the actual weight,
Substituting the known values,
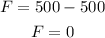
By the Newton's second law, the acceleration of the elevator is,
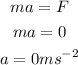
By the kinematics equation, the displacement in the time interval 0 to 5 seconds is,
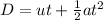
where D is the displacement, u is the initial velocity, a is the acceleration, and t is the time,
Substituting the known values,
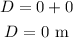
Thus, the displacement in the 0 to 5 seconds time interval is zero.
(b). For 5 to 10 seconds interval,
As the scale reading is 700 N, thus, the acceleration of the elevator is,
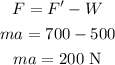
where m is the mass,
From the weight, the value of mass is,
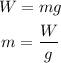
where g is the acceleration due to gravity,
Substituting the known values,
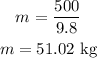
Thus, the acceleration of the elevator is,

By the kinematics equation, the displacement of the elevator is,
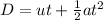
Substituting the known values,
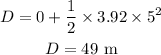
Thus, the displacement of elevator is 49 meters for the time interval 5 seconds to 10 seconds.
(c). For the time interval 10 seconds to 15 seconds,
The apparent weight (scale reading) is 500 N.
Thus, the acceleration of the elevator is,
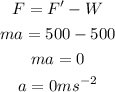
As the scale count is same as the normal weight, thus, elevator must not be moving or it is stopped at some height after moving some displacement upto 10 seconds. Thus, there will be no displacement of the elevator.
(d). For the time interval of 15 seconds to 20 seconds,
The apparent weight of the student is 300 N.
Thus, the acceleration of the elevator is,

Here, the negative sign indicates the elevator is moving in the downward direction.
By the kinematics equation, the displacement of the elevator in the time interval 15 to 20 seconds is,
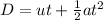
Substituting the known values,
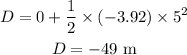
Here, the negatiev sign indicates the downward displacement,
Thus, the displacement of the elevator in the -49 meter.