It is given that the distance is 6 miles and the time is 2 hours upstream and one and a quarter hour downstream.
The time downstream is given by:
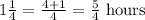
Since the distance is constant, it follows:

So the distance is constant hence:
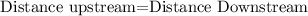
Let the speed of kayak be x and speed of current be y so the speed downstream is x+y and speed upstream is x-y so it follows:
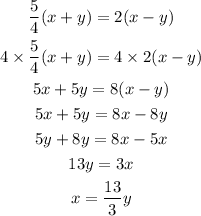
Use the individual equation to find x and y as follows:
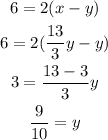
Hence the speed of the water current is 9/10 miles per hour.
The speed of the kayak is given by:
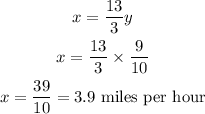
Hence the speed of the kayak without the water current is 3.9 miles per hour.
The time required without water current is:
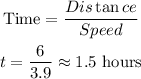
Hence it will take approximately 1.5 hours without the current.