Question

I keep get 35 and it wrong? Can you please help me ?

Answer 1

Given: 7 different jellybeans

To Determine: How many ways the 7 different jellybeans can be lined up in a row of 3

Solution

We are considering an arrangement, so we would be using the permutation formula

The permuation formula is as shown below

`_nP_r=(n!)/((n-r)!)`

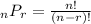
Applying the formula above to the given as shown below

`\begin{gathered} _7P_3=(7!)/((7-3)!) \\ _7P_3=(7*6*5*4!)/(4!) \\ _7P_3=7*6*5=210 \end{gathered}`

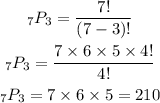
Hence, the different ways 7 different jellybeans be lined up in a row of 3 is 210ways