Question

there are 750 seats.the number of seats in a row is 5 less than the number of rows.how many seats are there in a row?

Answer 1

Given:

The total number of seats, T=750.

Let x be the number of seats in a row and y be the number of rows.

It is given that the number of seats in a row is 5 less than the number of rows.

Hence, the number of seats in a row can be expressed as,

`x=y-5\text{ ---(a)}`

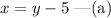
Now, expression for the total number of seats can be given by,

`T=xy`

Plug in x=y-5 and T=750 in the above equation and simplify.

`\begin{gathered} 750=(y-5)y \\ 750=y^2-5y \\ y^2-5y-750=0\text{ ---(1)} \end{gathered}`

The equation (1) is in the form of a quadratic equation of the form,

`ay^2+by+c=0\text{ ---(2)}`

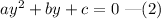
Comparing equations (1) and (2), a=1, b=-5 and c=-750.

Now, using discriminant method, the solution of y can be expressed as,

`\begin{gathered} y=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ y=\frac{-(-5)\pm\sqrt[]{(-5)^2-4*1*(-750)}}{2*1} \\ y=\frac{5\pm\sqrt[]{25+3000}}{2*1}\text{ } \\ y=\frac{5\pm\sqrt[]{3025}}{2} \\ y=(5\pm55)/(2)\text{ } \\ y=(5+55)/(2)\text{ or y=}(5-55)/(2) \\ y=(60)/(2)\text{ or y=}-(50)/(2) \\ y=30\text{ or y=-25} \end{gathered}`

Since the number of rows cannot be negative, y=30.

Put y=30 in equation (a) to find x.

`\begin{gathered} x=30-5 \\ x=25 \end{gathered}`

Therefore, the number of seats in a row is 25.