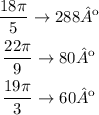The first thing we have to know is that pi= 180º
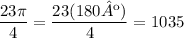
From this value of 1035 we must subtract 360 for each turn of the circumference until it gives us a value less than 360
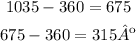
So the first answer would be
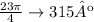
Using the same methodology the following angles would give