Given that :
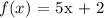
We can prove that :

is it's inverse doing the following:
Step 1. Set y = f(x):
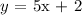
Step 2. Switch the variables:
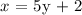
Then we solve for y:
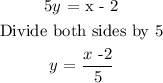
Step 3. The inverse of :
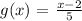
can be found in a similar way.
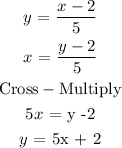
This tells us that f(x) and g(x) are one to one functions are f(x) is the mirror image of g(x)