Question

write an equation in slope intercept form for the line that passes through the given point and is perpendicular to the graph of the equation. (-4,2); y= -1/2x + 6

Answer 1

First of all we are going to find the slope perpendicular to the equation y = -1/2 x +6.

We need to remember that two slopes are perpendicular if its product is equal to -1. Like this:

`\begin{gathered} m_1\cdot m_2=-1 \\ m_1=-(1)/(2)_{} \\ m_2=-(1)/(m_1)=-(1)/(-(1)/(2))=2 \\ m_2=2 \end{gathered}`

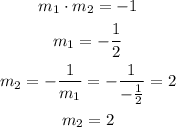
Now, we find the equation of the line using the general form:

`(y-y_1)=m(x-x_1);\text{ }`

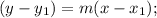
m - slope

`(x_1,y1)=(-4,2)_{}`

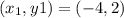
That was a point of the line, now:

`\begin{gathered} (y-2)=2(x-(-4)) \\ y-2=2x+8 \\ y=2x+10 \end{gathered}`

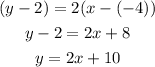
Finally, the equation of the line that passes through (-4,2) and is perpendicular to the equation y = -1/2x+6 is

y=2x+10