Question

I’m not quite sure on why I’m not getting the correct solution. Please help!The questions are A) what is the initial value of Q, when t = 0? What is the continuous decay rate? B) Use the graph to estimate the value of t when Q = 2 C) Use logs to find the exact value of t when Q = 2

Answer 1

The given exponential function is

`Q=11e^(-0.13t)`

The form of the exponential continuous function is

`y=ae^(rt)`

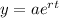
a is the initial amount (value y at t = 0)

r is the rate of growth/decay in decimal

Compare the given function by the form

`a=11`
`\begin{gathered} r=0.13\rightarrow decay \\ r=0.13*100\text{ \%} \\ r=13\text{ \%} \end{gathered}`

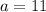
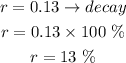
a)

The value of Q at t = 0 is 11 and the decay rate is 13%

The initial value of Q is 11

The continuous decay rate is 13%

From the graph

To find the value of t when Q = 2

Look at the vertical axis Q and go to the scale of 2

Move horizontally from 2 until you cut the graph

Go down to read the value of t

The value of t is about 13

b)

At

Q = 2

t = 13

c)

Now, we will substitute Q in the function by 2

`2=11e^(-0.13t)`

Divide both sides by 11

`(2)/(11)=e^(-0.13t)`

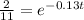
Insert ln on both sides

`ln((2)/(11))=lne^(-0.13t)`

Use the rule

`lne^n=n`
`lne^(-0.13t)=-0.13t`

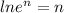
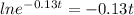
Substitute it in the equation

`ln((2)/(11))=-0.13t`

Divide both sides by -0.13

`\begin{gathered} (ln((2)/(11)))/(-0.13)=t \\ \\ 13.11344686=t \end{gathered}`

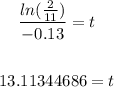
At

Q = 2

t = 13.11344686