To check if Triangles ABE, ADE, and CBE are congruent, let us compute for the distance of each line using the Distance Formula,
![\text{ }d\text{ = }\sqrt[]{(x_2-x_1)^2\text{ + (}y_2-y_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/4gwet41rrhm6vtl06gpbx2wqmrjdytszbd.png)
Where,
d = Distance
(x1, y1) = Coordinates of the first point
(x2, y2) = Coordinates of the second point
Let's compute the distance of the following lines:
Triangle ABE: Lines AB, AE, and BE
Triangle ADE: Lines AD, AE, and ED
Triangle CBE: Lines CE, CB, and BE
For Triangle ABE,
![\text{ d}_(AB)\text{ = }\sqrt[]{(-1-(-4))^2+(3-(-1))^2}\text{ = }\sqrt[]{(-1+4)^2+(3+1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/owkyge6xy8ilzyjqwhsy4nbaawfgtbpxoj.png)
![\text{ d}_(AB)\text{ = }\sqrt[]{(3)^2+(4)^2}\text{ = }\sqrt[]{9+\text{ 16}}\text{ = }\sqrt[]{25}](https://img.qammunity.org/2023/formulas/mathematics/college/k2blc5w7c4uc8itj98k01yzzztmz79gc3l.png)
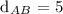
![\text{ d}_(AE)\text{ =}\sqrt[]{(1-\text{ }(-1))^2+(0\text{ - }(-4))^2}\text{ = }\sqrt[]{(1+1)^2+(0+4)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/xlg3pc6rqjfh5m2li348cuffs6xpmxfuo1.png)
![\text{ d}_(AE)\text{ = }\sqrt[]{(2)^2+(4)^2}\text{ = }\sqrt[]{4\text{ + 16}}](https://img.qammunity.org/2023/formulas/mathematics/college/p4iceec6w67msz9v8junyouvzl8xrpqky0.png)
![\text{ d}_(AE)\text{ =}\sqrt[]{20}](https://img.qammunity.org/2023/formulas/mathematics/college/4gmxp6q01keatnnssjc3okhcax9zoka1cx.png)
![\text{ d}_(BE)\text{ = }\sqrt[]{(1\text{ - (}3))^2+(0\text{ - (-1)})^2}\text{ = }\sqrt[]{(1-3)^2+(0+1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/fyapbvfa5xjs3yr7j6c04a4y0p43cfzglg.png)
![\text{ d}_(BE)=\text{ }\sqrt[]{(-2)^2+(1)^2}\text{ = }\sqrt[]{4\text{ + 1}}](https://img.qammunity.org/2023/formulas/mathematics/college/8077li24wilp0sqsi9kxax2rsua8o78o0f.png)
![\text{ d}_(BE)\text{ = }\sqrt[]{5}](https://img.qammunity.org/2023/formulas/mathematics/college/qe4wzvgmx8kxd6jymqutkvobtjzom0s1iv.png)
For Triangle ADE, let's compute for the distance of line AD and ED since we already got the distance of line AE.
![\text{ d}_(AD)\text{ = }\sqrt[]{(-1-(-1))^2+\text{ (}1\text{ - }(-4))^2}\text{ = }\sqrt[]{(-1+1)^2+(1+4)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/t5j5yo89zp9tc4zc6gjktp40b1f4u3yy8s.png)
![\text{ d}_(AD)\text{ = }\sqrt[]{(0)^2+(5)^2}\text{ = }\sqrt[]{25}](https://img.qammunity.org/2023/formulas/mathematics/college/3iaz76lm0kkigf2oi8dutr1ojg3to6wfsl.png)
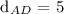
![\text{ d}_(ED)=\text{ }\sqrt[]{(-1\text{ - (}1))^2+(1-0)^2}\text{ = }\sqrt[]{(-1-1)^2+(1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/fwga8esss7ky4wcb2h9affy0w40mv35gpc.png)
![\text{ d}_(ED)\text{ = }\sqrt[]{(-2)^2_{}+(1)^2}\text{ = }\sqrt[]{4\text{ + 1}}](https://img.qammunity.org/2023/formulas/mathematics/college/ecft7e0lrekuuxifvha96hj8c2coceluz7.png)
![\text{ d}_(ED)\text{ = }\sqrt[]{5}](https://img.qammunity.org/2023/formulas/mathematics/college/g1sv1zkanhyrdg3jmunbn3l76dwecnskng.png)
For Triangle CBE, let's compute for the distance of line CE and CB since we already got the distance of line BE.
![\text{ d}_(CE)\text{ = }\sqrt[]{(3-\text{ }1)^2+(4-0)^2}\text{ = }\sqrt[]{(2)^2+(4)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/e2wfq7obm9zwm9k8a1tkrc7th1rkarjyh3.png)
![\text{ d}_(CE)\text{ = }\sqrt[]{4+16}\text{ = }\sqrt[]{20}](https://img.qammunity.org/2023/formulas/mathematics/college/r5elpnwf3k7sokl3nnvt9izd51uh2o37i0.png)
![\text{ d}_(CE)\text{ = }\sqrt[]{20}](https://img.qammunity.org/2023/formulas/mathematics/college/44npx5yybumfp3sbetqseeazpu93xyz5q3.png)
![\text{ d}_(CB)\text{ = }\sqrt[]{(3-3)^2+(4\text{ - (}-1))^2}\text{ =}\sqrt[]{(0)^2+(4+1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/2e2si1hkfpfwuo9jztuolz2ghyf256mxem.png)
![\text{ d}_(CB)\text{ =}\sqrt[]{(5)^2}\text{ = }\sqrt[]{25}](https://img.qammunity.org/2023/formulas/mathematics/college/on2e1icm8njvm3yjnhu7udifjdtsf3syik.png)
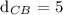
In summary,
Triangle ABE:
![AB=\text{ 5, AE = }\sqrt[]{20}\text{ and BE = }\sqrt[]{5}](https://img.qammunity.org/2023/formulas/mathematics/college/zm1sv1f1yx575gailnocxfm5ma6srrpwk0.png)
Triangle ADE:
![\text{ AD = 5, AE = }\sqrt[]{20}\text{ and ED = }\sqrt[]{5}](https://img.qammunity.org/2023/formulas/mathematics/college/l5ur2nd0682oqu1dgoezo5cu0p4cwysy29.png)
Triangle CBE: CE, CB, and BE
![\text{ CB = 5, CE = }\sqrt[]{20}\text{ and BE = }\sqrt[]{5}](https://img.qammunity.org/2023/formulas/mathematics/college/zo2m0ho7uoqnz68eyf5eplonemkyfjwx1t.png)
The sides of the three triangles shown in the grid are congruent based on the SSS Rule of Triangle.
Thus, the statement that meets our evaluation is:
D. Triangle ABE, ADE and CBE are all congruent.