Question

I need help solving this problem any help is appreciated

Answer 1

Step-by-step explanation

If we want to solve this problem we first need to list a few properties of trigonometric functions:

`\begin{gathered} \text{cot }\theta=(\cos\theta)/(\sin\theta) \\ \sin^2\theta+\cos^2\theta=1 \end{gathered}`

We are told that cot(θ)=1/2. Using the first equation and this data we obtain the following:

`(1)/(2)=(\cos\theta)/(\sin\theta)`

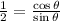
We multiply both sides and we get an expression for the cosine of θ:

`\begin{gathered} (1)/(2)\sin\theta=(\cos\theta)/(\sin\theta)\cdot\sin\theta \\ \cos\theta=(1)/(2)\sin\theta \end{gathered}`

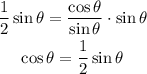
Now we are going to take the second property I wrote in the begining and replace the cosine of θ with this new expression that we found:

`\begin{gathered} \sin^2\theta+\cos^2\theta=\sin^2\theta+((1)/(2)\sin\theta)^2=1 \\ \sin^2\theta+(1)/(4)\sin^2\theta=1 \\ (5)/(4)\sin^2\theta=1 \end{gathered}`

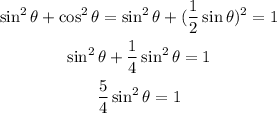
We must solve this equation for the sine of θ. We can multiply both sides by 4/5:

`\begin{gathered} (4)/(5)\cdot(5)/(4)\sin^2\theta=1\cdot(4)/(5) \\ \sin^2\theta=(4)/(5) \end{gathered}`

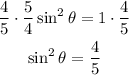
And we apply a square root to both sides:

`\begin{gathered} √(\sin^2\theta)=\sqrt{(4)/(5)} \\ |\sin\theta|=(2)/(√(5)) \end{gathered}`

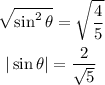
We are told that θ is located in quadrant I which means that its sine is positive. Therefore we get:

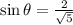
`\sin\theta=(2)/(√(5))`Answer

Then the answer is 2/√5