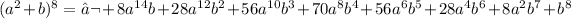For this exercise, we must use the binomial theorem. The formula of this theorem is described as follows
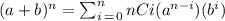
Where nCi represents the combinatory of n between i. For our case,
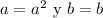
Replacing the values you have in the formula
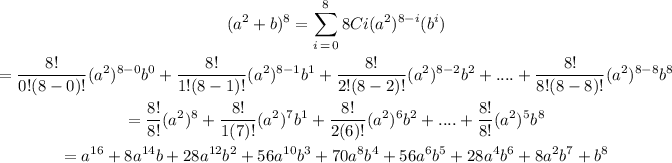
Thus,the expansion and simplification is as follows