A.
Pavilion's line:
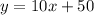
The slope of the line is the coefficient multiplying x, so it is m=10
Heliophobia's line:
To determine the slope of this line you have to use the following formula:
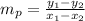
Where
(x₁,y₁) are the coordinates of one point on the line
(x₂,y₂) are the coordinates of a second point on the line
I'll choose to use points (1,85) and (0,70) but you can use any pair of points on the given line:
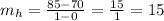
The slope of the Pavillion's line is m=10 → it indicates that y increases 10 units for every unit increase of x.
The slope of the Heliophobia's line is m=15 → it indicates that y increases 15 units for every unit increase of x.
The increase of Heliophobia's line is greater than the increase of Pavillion's line.
B.
The y-intercept is the value of y when x=0
For Pavillion's line the y-intercept is
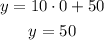
The coordinates are (0, 50)
For the Heliophobia's line the y-intercept is given in the table (0,70)