Question

The graph of a function is shown on the coordinate plane below. Which relationship represents a function with the same slope as the function graphed?

Answer 1

If (x_1, y_1) and (x_2, y_2) are points of a line, its slope is given by:

`m=(y_2-y_1)/(x_2-x_1)\text{.}`

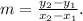
From the graph of the function, we see that the line passes through the points:

• (x_1, y_1) = (-1, 6),

,

• (x_2, y_2) = (0, 1).

The slope of the line is:

`m=(1-6)/(0-(-1))=-5.`

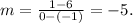
A) Using the points:

• (x_1, y_1) = (-2, 0),

,

• (x_2, y_2) = (2, 10).

We find that the slope of this line is:

`m=(10-0)/(2-(-2))=(10)/(4)=2.5.`

This function has not the same slope as the line of the graph.

B) The general equation of a line is:

`y=m\cdot x+b\text{.}`

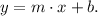
Where m is the slope and b is the y-intercept.

Comparing the general equation with the equation:

`y=-5x+3,`

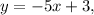
we see that the slope of the line of this equation is m = -5.

This function has the same slope as the line of the graph.

C) Using the points:

• (x_1, y_1) = (-4, 8),

,

• (x_2, y_2) = (0, 5).

We find that the slope of this line is:

`m=(5-8)/(0-(-4))=-(3)/(4)=-0.75.`

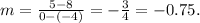
This function has not the same slope as the line of the graph.

D) Comparing the general equation with the equation:

`y=-(5)/(4)x+2.`

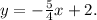
we see that the slope of the line of this equation is m = -5/4.

This function has not the same slope as the line of the graph.

Answer

B. y = -5x + 3