Solution:
Given the equation below
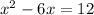
Applying the completing the square method
Where the general form of a quadratic equation is

For the completing square method,

Where
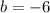
The number that should be added to both sides of the equation to complete the square is

Hence, the number is 9 (option B)