Hello there. To slve this question, we'll have to remembrer some properties about maximum and minimum in a quadratic function.
Given a quadratic function f as follows:

We can determine whether or not the vertex is a maximum or minimum by the signal of the leading coefficient a.
If a < 0, the concavity ofthe parabolai is facing down, hence it admits a maximum value at its vertex.
If a > 0, the concavity of the parabola is facing up, hence it admits a minimum value at its vertex.
As a cannot be equal to zero (otherwise we wouldn't have a quadratic equation), we use the coefficients to determine an expression for the coordinates of the vertex.
The vertex is, more generally, located in between the roots of the function.
t is easy to prove, y comlpleting hthe square, that the solutions of the equation

are given as

Taking the arithmetic mean of these values, we get the x-coordinate of the vertex:
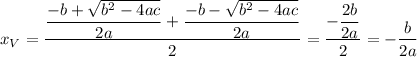
By evaluating the function at this point, we'll obtain the y-coordinate of the vertex:
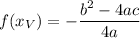
With this, we can solve this question.
Given the function:

First, notice the leadin coefficient is a = 2 , that is positive.
Hence it has a minimum point at its vertex.
To determine these coordinates, we use the other coefficients b = -12 and c = 19.
Plugging the values, we'll get
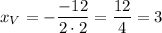
Plugging ths value in the function, ewe'll get
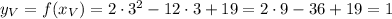
Hence we say that the final answer is
Vertex is a minimum point at (3, 1)
As you can see in the gaph.