Answer:
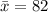
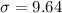
Explanation:
Given

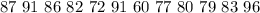
Solving (a); Point estimate of mean
To do this, we simply calculate the sample mean
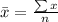
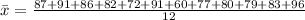
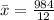
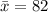
Solving (b); Point estimate of standard deviation
To do this, we simply calculate the sample standard deviation
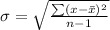
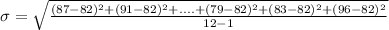
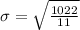
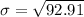
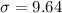
Note that: The sample mean and the sample standard deviation are the best point estimators for the mean and the standard deviation, respectively.
Hence, the need to solve for sample mean and sample standard deviation