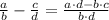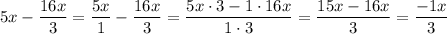Question

(d) 8x + 3y = -45x + 2y = 6Solve the following simultaneous linear equation

Answer 1

To solve the following simultaneous linear equation, we are going to solve for y on the first equation and replace it on the second as:

`\begin{gathered} 8x+3y=-4 \\ 3y=-4-8x \\ y=(-4-8x)/(3) \\ y=(-4)/(3)-(8x)/(3) \end{gathered}`

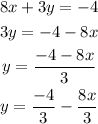
Replacing it on the second equation and solving for x, we get:

`\begin{gathered} 5x+2y=6 \\ 5x+2((-4)/(3)-(8x)/(3))=6 \\ 5x-(8)/(3)-(16x)/(3)=6 \\ 5x-(16)/(3)x=6+(8)/(3) \\ (-1)/(3)x=(26)/(3) \\ -x=26 \\ x=-26 \end{gathered}`

Finally, replacing x on the first equation and solving for y, we get:

`\begin{gathered} 8x+3y=-4 \\ 8(-26)+3y=-4 \\ 3y=-4+208 \\ 3y=204 \\ y=(204)/(3)=68 \end{gathered}`

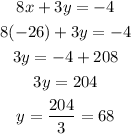
Answer: x = -26 and y = 68

To make subtraction of 5x - 16x/3, we can use the following equation:

`(a)/(b)-(c)/(d)=(a\cdot d-b\cdot c)/(b\cdot d)`
`\begin{gathered} 5x-(16x)/(3)=(5x)/(1)-(16x)/(3)=(5x\cdot3-1\cdot16x)/(1\cdot3)=(15x-16x)/(3)=(-1x)/(3) \\ \end{gathered}`