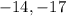Question

=O GRAPHINGFinding the next terms of an arithmetic sequence with integersThe first three terms of an arithmetic sequence are as follows.-5, -8, -11Find the next two terms of this sequence.5.-8.-11.008 OBx 6

Answer 1

Given the first three terms of an arithmetic sequence as;

`-5,-8,-11`

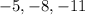
An arithmetic sequence is a sequence with a common difference d, The common difference is the difference between two consecutive terms. Where;

`\begin{gathered} d=a_2-a_1 \\ \text{Where;} \\ a_2=\text{ second term;} \\ a_1=\text{first term} \end{gathered}`

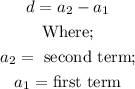
Thus;

`\begin{gathered} d=-8-(-5) \\ d=-8+5 \\ d=-3 \end{gathered}`

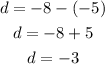
Also, the next term of the sequence can be known by adding the common difference to the previous term.

Hence, the next two terms are;

`\begin{gathered} =-11+(-3) \\ =-11-3 \\ =-14 \\ \text{and } \\ =-14+(-3) \\ =-14-3 \\ =-17 \end{gathered}`

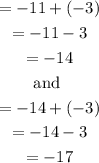
FINAL ANSWER:

`-14,-17`