We are given the following function of distance in terms of time:
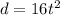
Where:
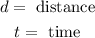
We are asked to determine the time when the distance is 4ft. To do that we will solve for "t". First, we will divide both sides by 16:
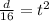
Now, we take the square root to both sides:
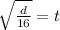
Simplifying we get:
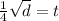
Now, we substitute the value of the distance:
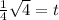
Solving the operations:
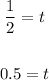
Therefore, the time is 0.5
The same procedure is used to determine the time for 64 feet.