Answer:
Step-by-step explanation:
Here, we want to get the number of mg of the atom that would remain
Half-life refers to the time taken for exactly half the mass of a radioactive isotope to be lost to radiation
From the question, the half-life is 6 hours
During the first six hours, we have a mass of 60 mg left
In the next 6 hours, which is the second half-life, we have 30 mg left
In the next 6 hours, which is the third half-life, we have 15 mg left
Now, for the next 5 hours, there will not be a complete decay
Thus, we get the decay constant using the following:
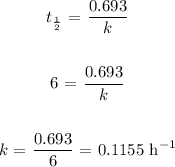
Mathematically: