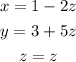Question

The matrix associated with the solution to a system of linear equations in x, y, and z is given. Write the solution to the system if it exists. Write an exact answer in simplified form. If there are infinitely many solutions, write an expression involving z for each coordinate where z represents all real numbers.

Answer 1

`\begin{gathered} x+2z=1 \\ y-5z=3 \end{gathered}`

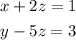
The solution is:

`\begin{gathered} x=1-2z \\ y=3+5z \\ z=z \end{gathered}`

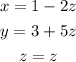
Explanation:

We must convert the matrix into a system of linear equations.

Each vertical represents the letters x, y and z, the first the x, the second y and the third the z. The fourth value is the value of the independent term that would be equal to the other expression, just like this:

`\begin{gathered} 1x+0y+2z=1 \\ 0x+1y-5z=3 \\ 0x+0y+0z=0 \end{gathered}`

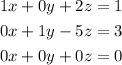
We operate and the system will finally be like this

`\begin{gathered} x+2z=1 \\ y-5z=3 \end{gathered}`

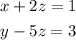
let's solve the system and we have:

`\begin{gathered} x=1-2z \\ y=3+5z \\ z=z \end{gathered}`