Question

The graph of y = x 2 has been translated 7 units to the left. The equation of the resulting parabola is _____.y = (x - 7) 2y = (x + 7) 2y = x 2 - 7y = x 2 + 7

Answer 1

The translation of a function to the left or to the right is a horizontal translation. Horizontal translation can be defined as the movement toward the left or right of the graph of a function by the given units. It should be noted that the shape of the function remains the same. The horizontal translation is also known as the movement/shifting of the graph along the x-axis. For any base function f(x), the horizontal translation by a value k can be given as

`f(x)=f(x\pm k)`

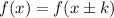
If the function is shifted to the right, the translation function would be

`f(x)=f(x-k)`

If the function is shifted to the left, the translation would be

`f(x)=f(x+k)`

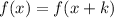
If the graph of y = x² has been translated 7 units to the left. The equation of the resulting parabola would be

`y=(x+7)^2`

Hence the equation of the resulting parabola is (x+7)²