Answer:
a) Common ratio = 2/7
b) First term = 135/7
Explanations:
The formula for finding the sum of a geometric progression is expressed as:
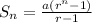
Since the sum of the first two terms is 15, then
S2 = 15
n = 2
Substitute into the formula:
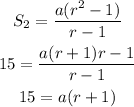
Also, the sum to infinity of a geometric sequence is expressed as:
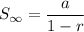
Substitute the given values into the formula:
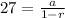
Solve both expressions simultaneously

Divide both expressions to have:

Cross multiply and solve for the common ratio "r"
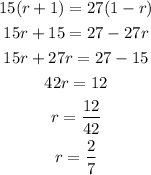
Hence the value of the common ratio is 2/7
b) Get the first term of the sequence;
Using the formula:
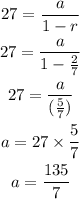
Hence the first term of the sequence is 135/7