We are given that the area of triangle AEC = 63 centimeters squared.
Since segment CD equals segment DB that means that triangle CDA and triangle BDA have the same area, and also triangle CDE and triangle BDE have the same area. This means mathematically the following:
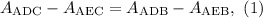
Also

Replacing equation (1) in equation (2)
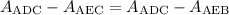
Simplifying
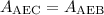
Therefore:
![A_{\text{AEB}}=63\operatorname{cm}^2]()
Since segments DE and EA is the same, then:
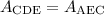
Therefore:
![A_{\text{CDE}}=63\operatorname{cm}^2]()
Since
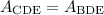
We have:
![A_{\text{BDE}}=63\operatorname{cm}^2]()
therefore, the area of the triangle is:

Replacing the known values:
![\begin{gathered} A_{\text{ABC}}=68+68+68+68=4(68) \\ A_{\text{ABC}}=272\operatorname{cm}^2 \end{gathered}]()