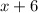Given:
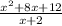
Let's divide the polynomials.
To divide, let's factorize the polynomial in the numerator.
Factorize using the AC method.
Find a pair of numbers whose product is 12 and whose sum is 8.
Thus, we have the numbers:
2 and 6
The factors of the polynomial in the numerator are:
(x+2) and (x+6)
We have:
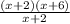
Now, cancel the common factors:
Therefore, the quotient after dividing the polynomials is = x + 6
ANSWER: