Given:
The equation of the hyperbola is given as,
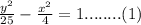
The objective is to graph the equation of the hyperbola.
Step-by-step explanation:
The general equation of hyperbola open in the vertical axis of up and down is,
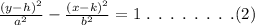
Here, (h,k) represents the center of the hyperbola.
The focal length can be calculated as,
![c=\sqrt[]{a^2+b^2}\text{ . . . . (3)}](https://img.qammunity.org/2023/formulas/mathematics/college/qlg05sfqy1zwujmftd256vnju2jj179pi3.png)
On plugging the values of a and b in equation (3),
![\begin{gathered} c=\sqrt[]{5^2+2^2} \\ =\sqrt[]{25+4} \\ =\sqrt[]{29} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/jxgeyr1o4g9pl2eylv513zah1q12lnd61r.png)
The foci can be calculated as,
![\begin{gathered} F(h,k\pm c)=F(0,0\pm\sqrt[]{29}) \\ =F(0,\pm\sqrt[]{29}) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/xn8csxtbv8dccyws4zamf4h6zm8kzftlrt.png)
The vertices can be calculated as,
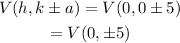
To obtain graph:
The graph of the given hyperbola can be obtained as,
Hence, the graph of the given hyperbola is obtained.