In similar triangles, corresponding sides are always in the same ratio.
Find the ratio of corresponding sides in the given triangles, to identify corresponding sides the greater side in one triangle is corresponding with the greater side of the other triangle.
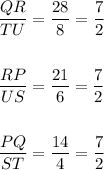
As the ratio of corresponding sides is the same, triangle PQR is similar to triangle STU
For similar triangles the corresponding angles are equal.
Corresponding angles for triangles PQR and STU:
P and S
Q and T
R and U
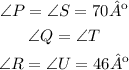
The sum of the interior angles in any triangle is always 180º:
