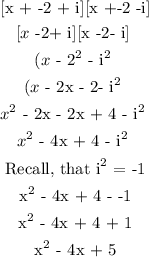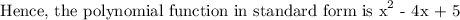Question

Write the polynomial function in standard form that has complex roots -2+i and -2-i

Answer 1

`\text{ x}^2\text{ - 4x + 5}`

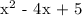
Step-by-step explanation

Given information

The root of the polynomial function are -2 + i and -2- i

To find the standard form of the polynomial function, follow the steps below

Step 1: Express the root of the polynomial in terms of the factor

`\begin{gathered} \text{ Given that the roots of the polynomial function are -2+i and -2 - i} \\ \text{ The factors of the above roots can be expressed as} \\ \text{ \lbrack x + \lparen-2 + i\rparen\rbrack and \lbrack x + \lparen-2 - i\rparen\rbrack} \end{gathered}`

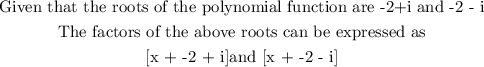
Step 2: Expand the factors of the polynomial in step 1

`\begin{gathered} \text{ \lbrack x + \lparen-2 + i\rparen\rbrack \lbrack x +\lparen-2 -i\rparen\rbrack} \\ [x\text{ -2\rparen + i\rparen\rbrack \lbrack x -2\rparen - i\rparen\rbrack} \\ (x\text{ - 2\rparen}^2\text{ - i}^2 \\ (x\text{ - 2\rparen\lparen x - 2\rparen- i}^2 \\ x^2\text{ - 2x - 2x + 4 - i}^2 \\ x^2\text{ - 4x + 4 - i}^2 \\ \text{ Recall, that i}^2\text{ = -1} \\ \text{ x}^2\text{ - 4x + 4 - \lparen-1\rparen} \\ \text{ x}^2\text{ - 4x + 4 + 1} \\ \text{ x}^2\text{ - 4x + 5} \end{gathered}`
`\text{ Hence, the polynomial function in standard form is x}^2\text{ - 4x + 5}`